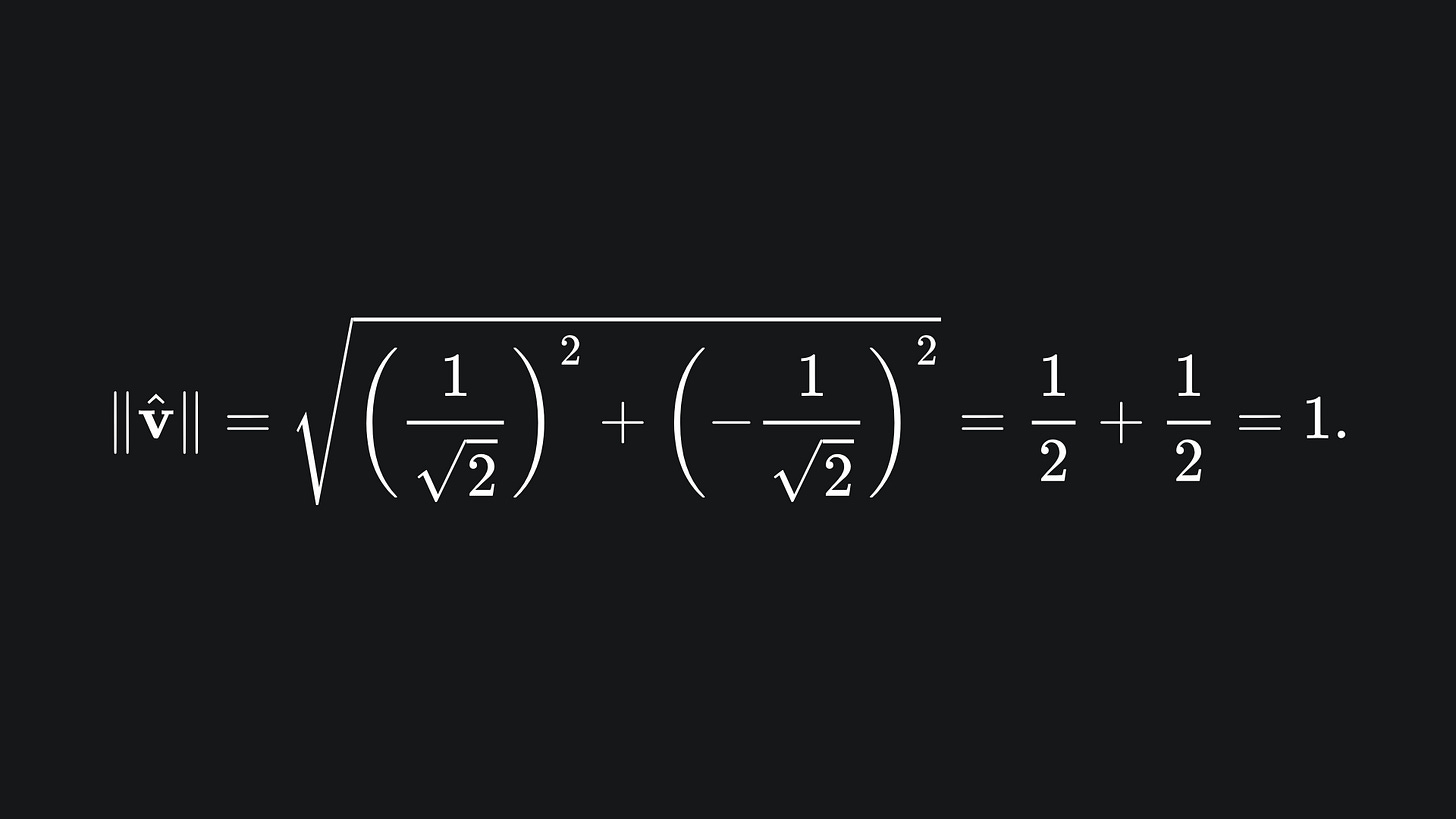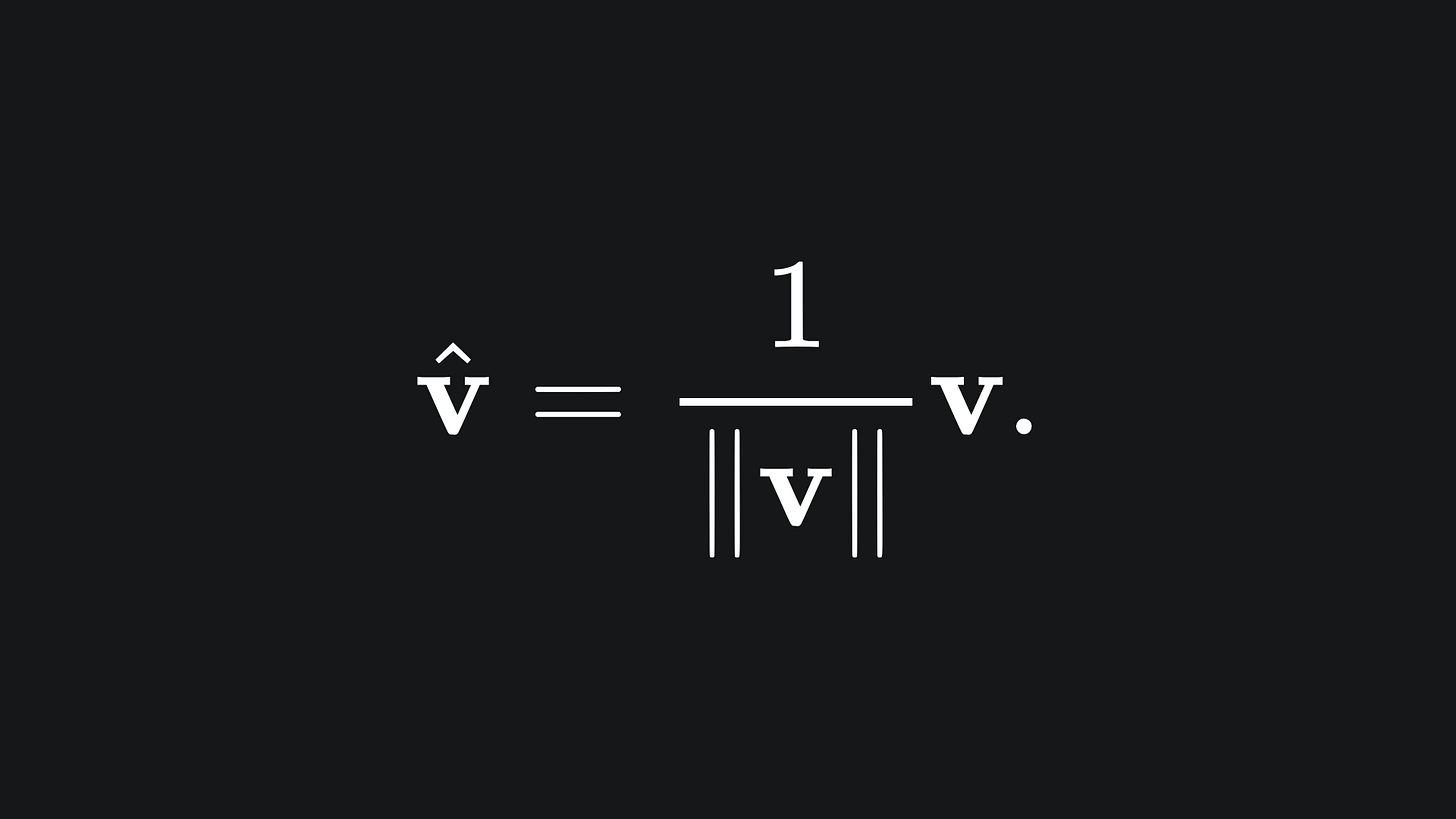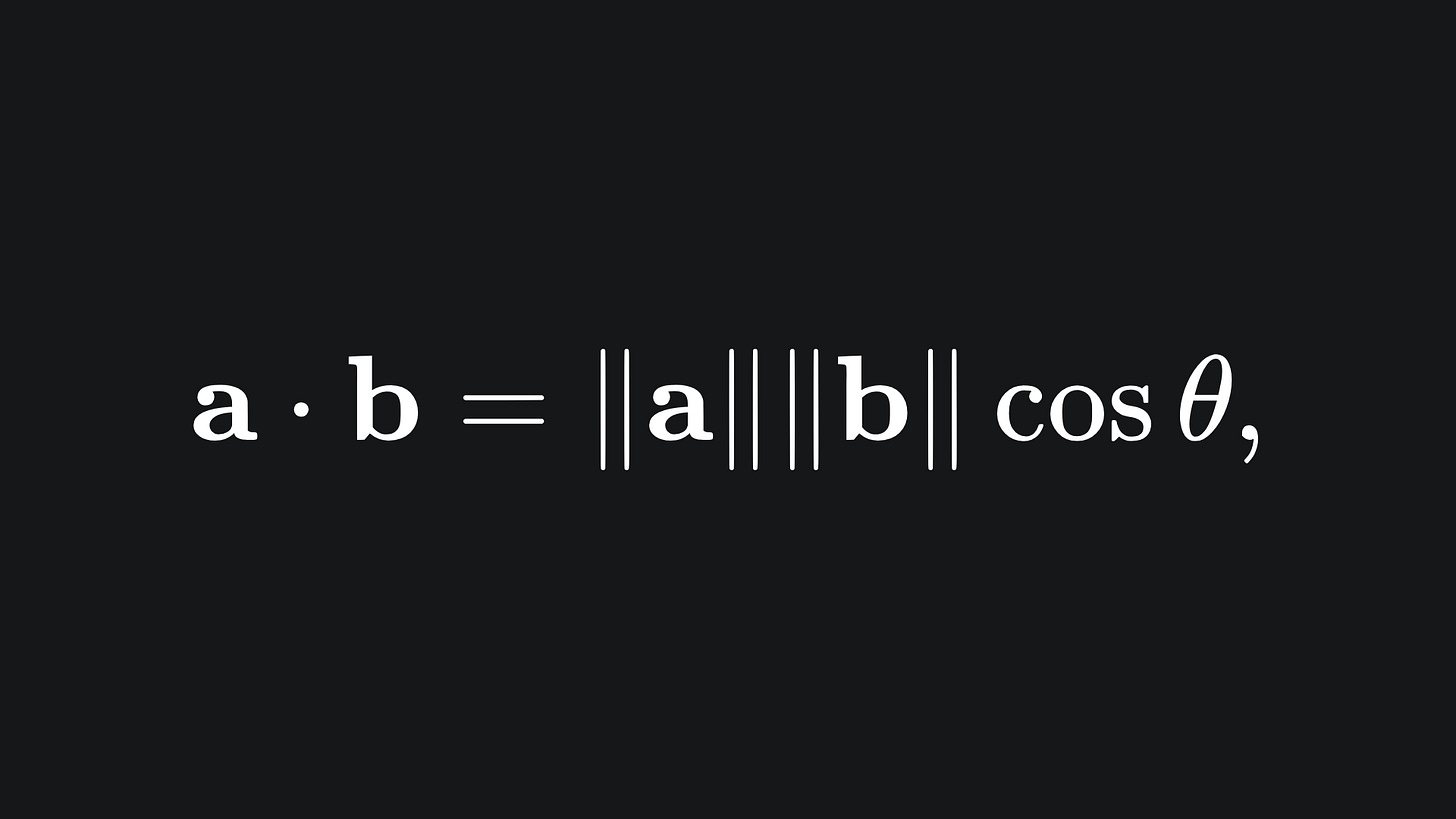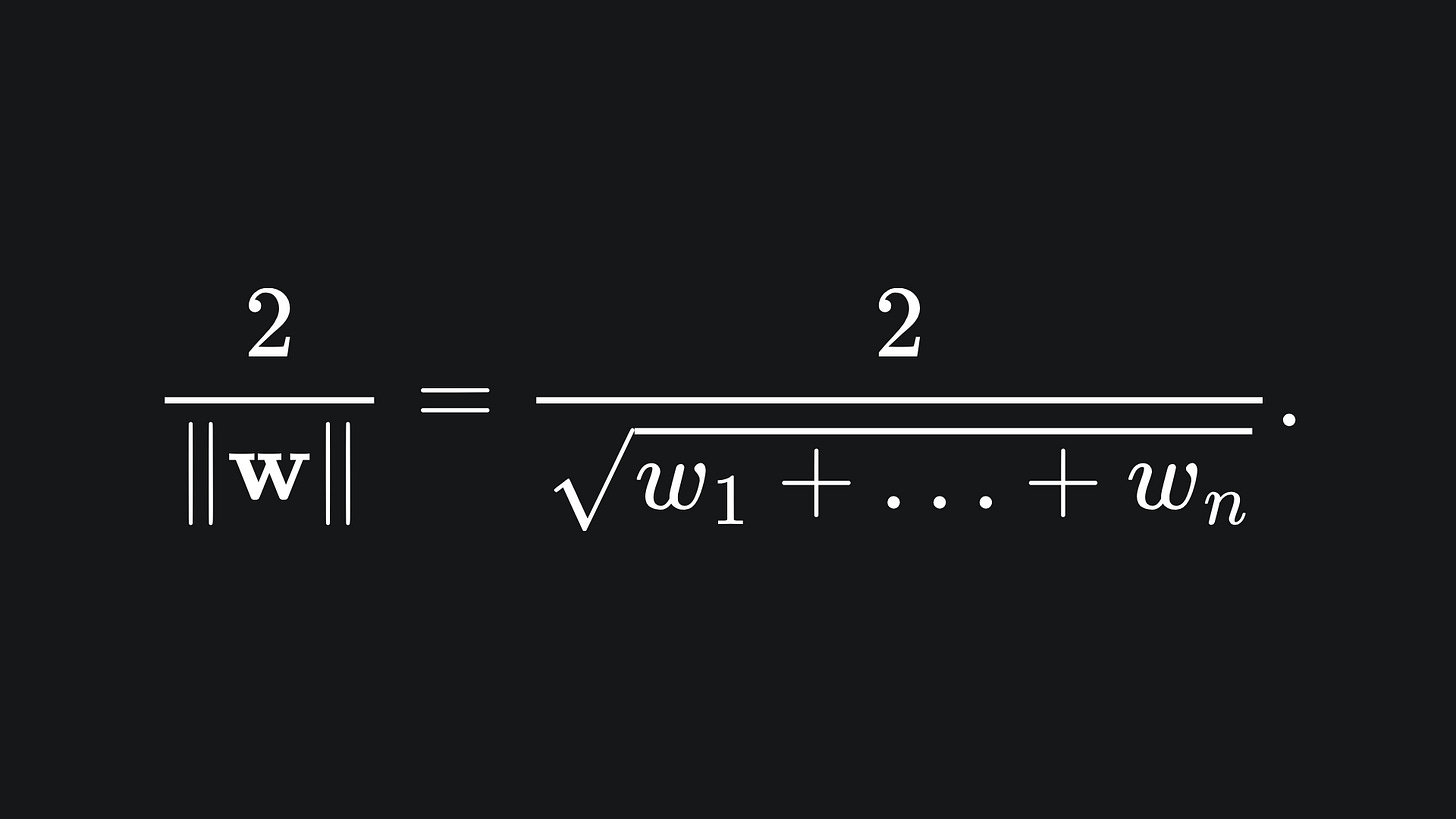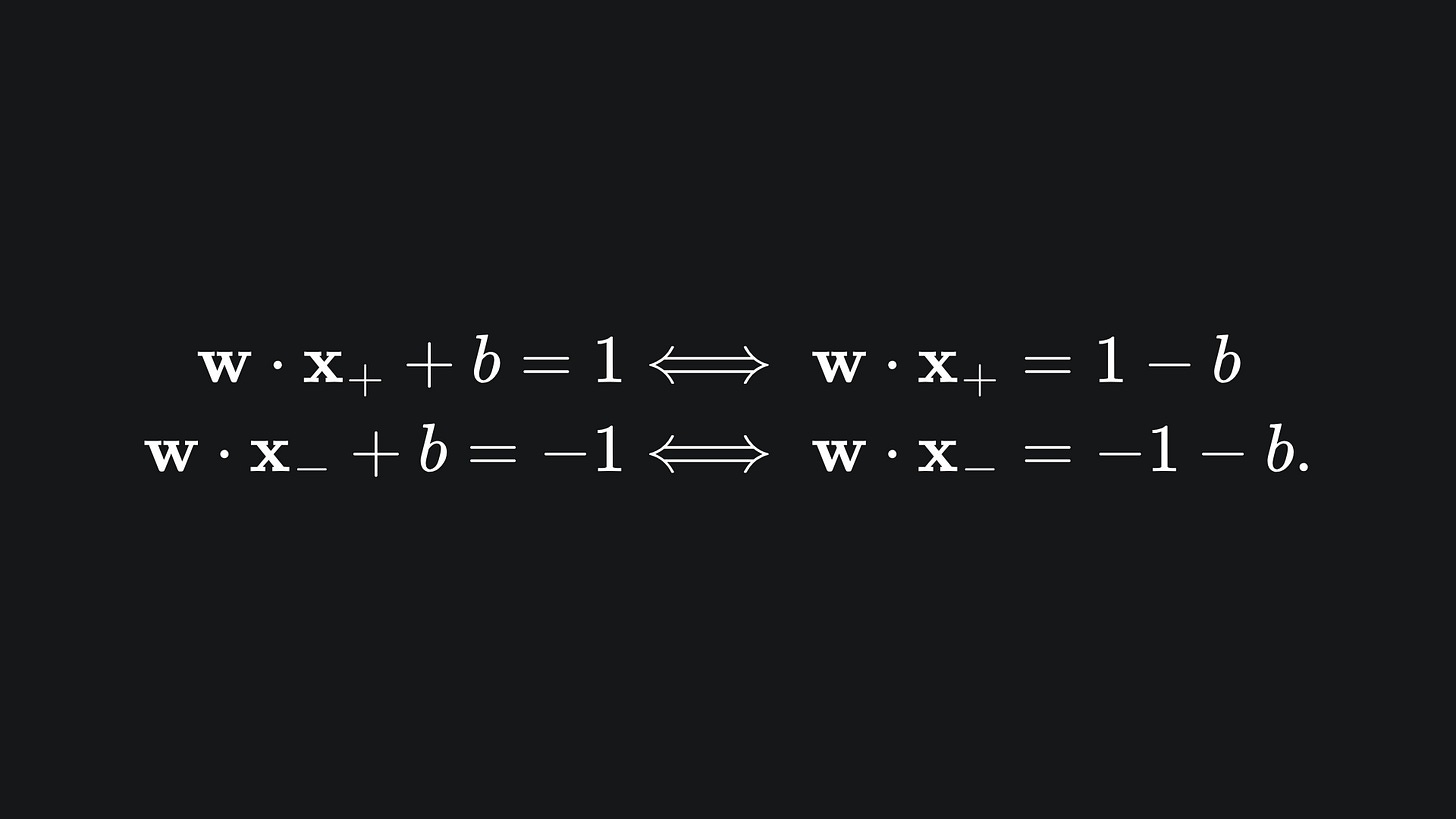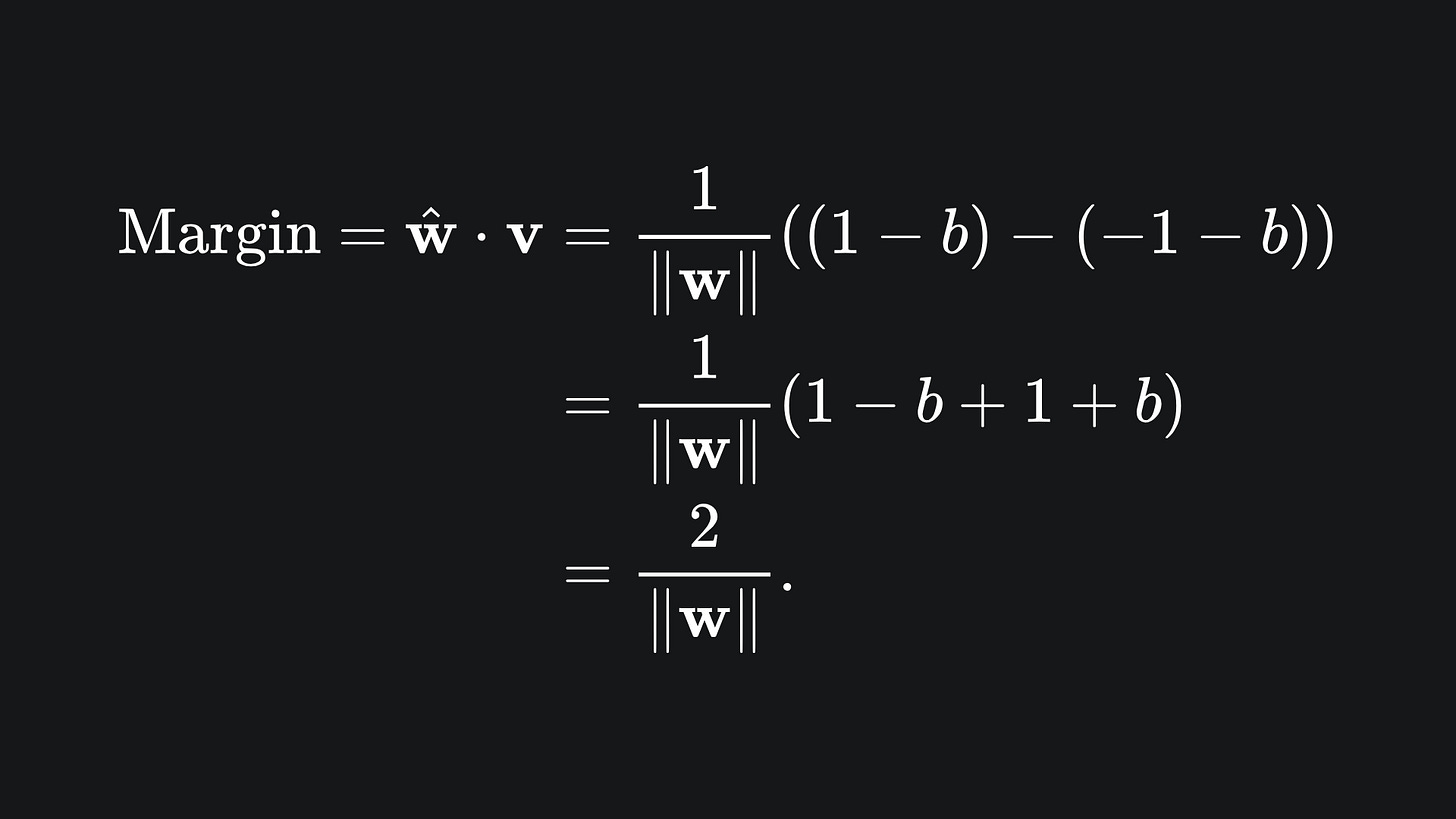Deriving the formula for the SVM's margin with three vector tools

Projections, unit vectors and dot products explained and used to derive a formula for the margin of the Support Vector Machine.

Hello fellow machine learners,

As of publishing this article, we’ve made it to the month of February. So if you started a New Year’s resolution last month, here’s a quick reminder to keep going 🤙🏼

Last week, we introduced the Support Vector Machine, a binary classification algorithm. We defined the support vectors and margin of the SVM, and covered some prerequisite foundations of geometry.

This week, we will cover some super useful vector tools that we will then apply to derive the formula for the margin of the SVM.

Time to get stuck in!

Some more vector preliminaries

We require some vector tools on top of those we encountered last week. In particular, I would like to cover three more concepts:

• Horizontal and vertical projections

• Unit vectors

• Dot products

The combination of these three ideas will help us understand the SVM margin in all its glory. Let’s do this!

1. With some simple trigonometry, any vector v can be broken down into a horizontal component and a vertical component. The formulas for these components are given in the below image:

   

   Decomposing the vector v into its horizontal and vertical components.

   Here, θ is the angle between the vector v and the horizontal.

2. A unit vector is a vector of length 1. To obtain a unit vector from a vector of arbitrary length, we just divide the vector by its magnitude. We usually denote unit vectors with a hat like ‘^’. As an example, the unit vector representation of the vector v = (1, -1) is

\(\hat {\textbf v} = \frac{1}{\sqrt{1^2+(-1)^2}}\cdot \begin{pmatrix} 1 \\ -1 \end{pmatrix} = \begin{pmatrix} \frac{1}{\sqrt 2} \\ \frac{-1}{\sqrt 2} \end{pmatrix}.\)

We can verify that the length of this unit vector is indeed 1:

\(\| \hat{\textbf v} \| = \sqrt{\left(\frac{1}{\sqrt 2}\right)^2 + \left(-\frac{1}{\sqrt 2}\right)^2} = \frac{1}{2} + \frac{1}{2} = 1.\)

So to create a unit vector from an arbitrary vector v, we can follow the formula

\(\hat{\textbf v} = \frac{1}{\| \textbf v \|} \textbf v.\)

3. Now for the dot product. The dot product takes two vectors as input and returns a scalar value. The formula for the dot product between the vectors a and b is given by

\(\textbf a \cdot \textbf b = \| \textbf a \| \| \textbf b \| \cos \theta,\)

where θ is the angle between the two vectors.

In particular, the horizontal projection a · cosθ from (1.) is given when b is taken to be the horizontal unit vector (1,0), and the vertical projection a · sinθ is given when b is taken to be the vertical unit vector (0,1).

We’re not going to worry too much about the value of θ explicitly today.¹

Now, things get crazy if we combine these three ideas: if we take the dot product between a vector v and a unit vector, say n̂, then the dot product will give us the scalar projection of the vector v in the direction of the vector n̂. Here is what this looks like:

Note: the dot product takes a pair of vectors and returns a scalar. So in the animation, the dot product gives us the length of the green double arrow.²

Margin formula: visual intuition

Recall that the margin of the SVM is the distance between each support and the decision boundary. Last week, I claimed that this is given by

\(\frac{2}{\| \textbf w \|} = \frac{2}{\sqrt{w_1+\dotsc+w_n}}.\)

It’s time for me to put my money where my mouth is 🤑🤑

There are a few ways to derive the formula. What we will do here is find the shortest distance between the hyperplanes wx+b=1 and wx+b=-1. This distance is equivalent to the sum of the distances between S+/S- and the decision boundary, which is what we want. (Recall that S+ is the vector closest point above the decision boundary, and S- is the closest point below.)

Let us denote the vector representations of these supports as x+ and x- respectively.

Define the vector v = (x+) - (x-). If we start this vector from the point S-, then the vector v takes us from x- and leads us straight to x+. This is shown by the pink vector in the below animation:

Okay nice, so if we find the length of the vector v, then we’re done, right?

Well, not quite. If v is not precisely perpendicular to the hyperplanes, then it will be longer than the actual distance between them.

But recall from last week that the vector w is precisely perpendicular to the decision boundary wx+b=0. Our two supporting hyperplanes are parallel to this boundary, hence w is perpendicular to these hyperplanes as well.

So if we could find the projection of the vector v along the vector w, then we will have achieved our goal…

…does that phrasing sound familiar?

Indeed, we can use what we learned earlier in this article to get the job done! Namely, if we take the dot product of v with a unit vector in the direction of w (which we will call ŵ), then we’ll have our margin formula!

And better yet, we already know how to get our unit vector ŵ; we simply divide w by its magnitude:

The length of the double arrow at the end of the animation is precisely the margin, which we claim is given by v · ŵ.

Margin formula: derivation with maths

As my maths professors at uni would always say, “A picture is NOT a proof”. Let’s not disappoint them:

\(\begin{align} \text{Margin = } \hat{\textbf w} \cdot \textbf v & = \frac{1}{\| \textbf w \|} \textbf w \cdot \textbf v & \text{(Unit vector form for w)} \\ & = \frac{1}{\| \textbf w \|} \textbf w \cdot (\textbf x_+ - \textbf x_-) & \text{(Definition of v)} \\ & = \frac{1}{\| \textbf w \|} (\textbf w \cdot \textbf x_+ - \textbf w \cdot \textbf x_-). \end{align}\)

Since S+ lies on the hyperplane wx+b=1 and S- lies on wx+b=-1, we know that

\(\begin{align} \textbf w \cdot \textbf x_+ + b = 1 & \iff \textbf w \cdot \textbf x_+ = 1-b \\ \textbf w \cdot \textbf x_- + b = -1 & \iff \textbf w \cdot \textbf x_- = -1-b. \end{align}\)

So we can plug these into the previous equation to end up with:

\(\begin{align} \text{Margin = } \hat{\textbf w} \cdot \textbf v & = \frac{1}{\| \textbf w \|} ((1-b)-(-1-b)) \\ & = \frac{1}{\| \textbf w \|} (1-b+1+b) \\ & = \frac{2}{\| \textbf w \|}. \end{align}\)

Mic drop.

Packing it all up

Believe it or not, there’s even more for us to unpack with the SVM! But it’ll have to wait until next week. In the meantime, let’s consolidate what we’ve learned this week:

• We can construct a unit vector from any arbitrary vector by dividing the vector by its magnitude.

• When the dot product is applied between a vector v and a unit vector, the result gives us the magnitude of the vector v in the direction of the unit vector.

• The size of the SVM’s margin depends entirely on the vector w.

Training complete!

I really hope you enjoyed reading!

Do leave a comment if you’re unsure about anything, if you think I’ve made a mistake somewhere, or if you have a suggestion for what we should learn about next 😎

Until next Sunday,

Ameer

PS… like what you read? If so, feel free to subscribe so that you’re notified about future newsletter releases:

Sources

• Lectures notes from Imperial College London, see chapter 3 for SVM: https://www.doc.ic.ac.uk/~dfg/ProbabilisticInference/InferenceAndMachineLearningNotes.pdf

1. But θ certainly has its uses in other contexts/algorithms.

2. Generally I will use arrows to indicates vectors, and double arrows to indicate lengths.