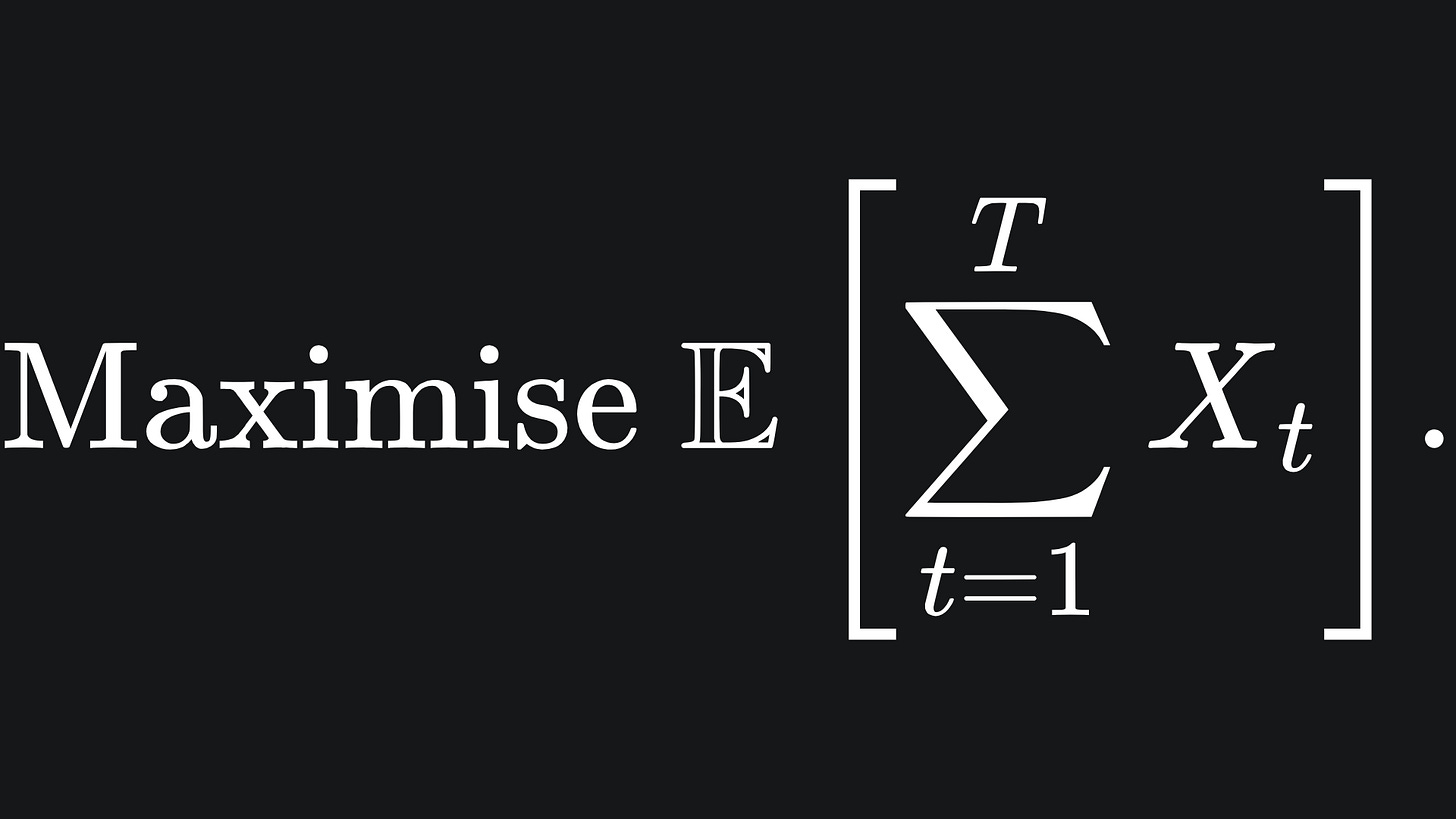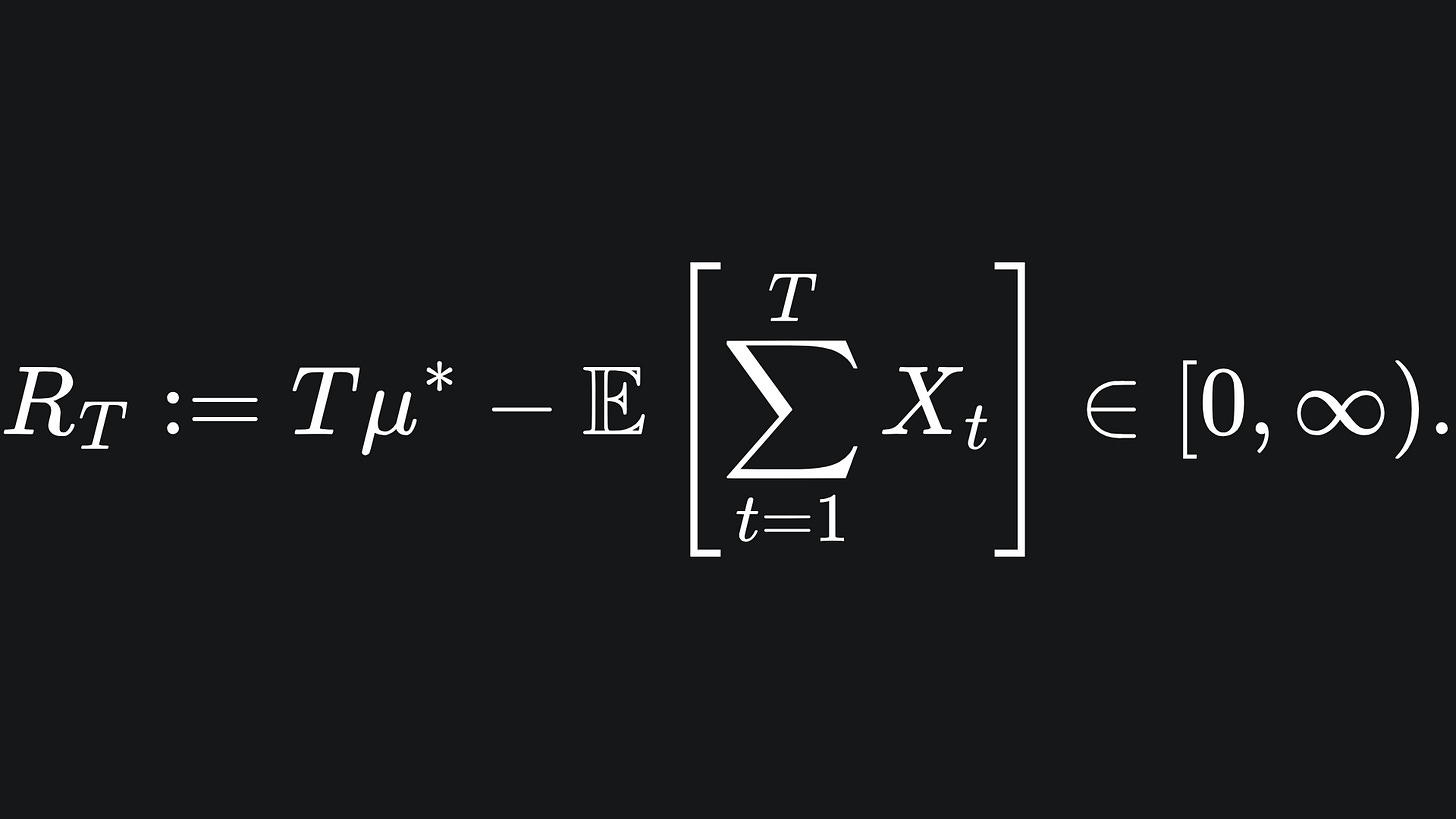An introduction to reinforcement learning with Multi Armed Bandits (MAB)

Agent-environment interactions, exploration vs exploitation and the epsilon-greedy algorithm for playing with Gaussian bandits.

Hello fellow machine learners,

Last week, we went knee-deep into the waters of Gaussian Mixture Models. It was quite a banger if I do say so myself, although you won’t need it to understand this article:

Today, we shall discuss a paradigm of machine learning quite unlike any that we have discussed before. Over the past few months, we have unpacked

🤖 Supervised learning: the model learns from a labelled dataset, with the goal of predicting what labels ought to be assigned to new unlabelled records.

🤖 Unsupervised learning: we present the model with an unlabelled dataset, and trust it to identify patterns in the data.

Now, what if we don’t have concrete labels for our data, but rather a set of actions that the computer can choose from?

Think of what would happen if you tried to train a computer to play chess, for example. How good a played chess move is depends almost entirely on where all the pieces are on the board, how many pieces have been captured on each side, and so on. Immediately capturing the opponent’s pieces isn’t always the right thing to do, because this can compromise the structure of your own pieces. Sometime, an action that is typically good can actually be ‘bad’ Or at least, there might be a better option.

Enter reinforcement learning, a paradigm of machine learning that exists somewhere between supervised and unsupervised. Reinforcement learning commonly involves an ‘agent’ (i.e. the computer) interacting with an ‘environment’, with the goal of taking actions in that environment in order to maximise some sort of reward. Today, we will introduce this idea through the Multi Armed Bandits problem, which forms the foundation of a lot of reinforcement learning theory.

😎 With that said… let’s get to unpacking a new ML concept 😎

Multi Armed Bandits: setup

Imagine the following scenario: there are three levers in front of you, each of which gives you a monetary value when pulled. But you don’t what the rewards are for each lever, only that each lever samples rewards from a distint Gaussian distribution. So for example, if the first lever followed a Gaussian distribution of mean 10 and variance 4, then the expected reward for pulling the first lever is $10, but most lever pulls will net you a reward in the range of $4 and $16.

We play a game of T rounds, where you are allowed to pull exactly one lever in each round. What strategy would you use in order to get the largest monetary rewards possible?

This setup is complemented well with some maths that will be helpful in future articles. We will use i to index the arms (levers) and t to index the rounds. Let:

• A_t denote the player’s arm choice at round t. So in the context of three levers, A_t takes a value in {1, 2, 3} for each value of t.

• X_t denote the reward received at round t (this will be distributed following the corresponding Gaussian arm).

• μ_i denote the mean reward of arm i. We also let i* denote the index of the optimal lever, with corresponding optimal mean reward set as μ*=μ_i. Recall that you as the player do not know the value of i*, but the aim is to figure this out with a good enough strategy.

Our goal is to maximise the mean reward over the T rounds:

Of course, if we knew the value of i*, we could just choose arm A_t=i* for every round t, bagging us an optimal total reward of Tμ*.

If we do not play absolutely optimally (which is almost guaranteed when we initially have no knowledge of the environment), then we can define the regret of our lever choices as

So if we chose the most optimal arm every time, the second term becomes equal to Tμ*, incurring a regret of 0.

As mentioned earlier, reinforcement learning often involves an agent-environmental interactions. In this bandit setup, you are the agent, and the environment corresponds to the number of levers, as well as the distributions from which the rewards are sampled.

The ‘best strategy’ will depend a lot on the distributions of the arms’ rewards, but for now, consider how you’d play this game before reading on…

Exploration vs Exploitation

A simple strategy to play this game could be exploration, where we pull each lever the same number of times. This could be done in whatever order you like, so long as you pull the first lever T/3 times, the second lever T/33 times, and the third lever T/33 times.¹

✅ Simple strategy

✅ Guaranteed to pull the most optimal lever

💭 Strategy does not take the observed rewards into account

💭 Pulls the most optimal lever the same number of times as the least optimal lever. Could we do better?

Another way to play would be to start by pulling each lever, say, n=10 times, and then exploit the arm that yields the greatest empirical reward. So if the second arm yielded the largest empirical reward after the trial of 30 pulls, then you could commit to that specific arm for the remaining 70 rounds of the game.

✅ Takes the observed rewards into account within the strategy

💭 How to decide the value of n?

Now, would it be good to instead interleave the way we explore or exploit the levers, rather than committing to exploration for a fixed number of initial rounds and exploiting thereafter? Enter…

The epsilon-greedy algorithm

The final strategy we’ll talk about today aims to combine the benefits of exploration and exploitation in a simple yet effective way. We begin by defining a parameter ε in between 0 and 1. For each round, we draw a value from a standard Gaussian distribution, let’s call the value x. Now:

if x < ε:
     Draw a reward from a random lever
else:
     Draw a reward from the lever we currently believe to be the most optimal

If the value of ε is small, then we will exploit far more often than we explore. Conversely, if ε is large, then we will be exploring more and exploiting less. This strategy is useful, because we can reap the benefits of exploring and exploiting throughout the rounds. The more rounds we play, the more information we will gain from exploration, which we can hopefully put to work during the exploitation rounds.

I have put together an animation to depict how this might work in practice. Don’t forget though- the success of these types of algorithms depends a lot on the environment you’re working in. For this animation, I used three Gaussian levers or parameters (2, 0.8), (5, 1.2) and (7, 0.5) respectively, so the setup is somewhat contrived. That said, check out the full source code here if you want to play around with it yourself 😄

(Edit: the following video now has a voiceover!)

Packing it all up

That’s all for today’s introduction to reinforcement learning. We will (hopefully) spend a bit of time comparing some bandit algorithms, as well as the different stochastic environments they can be played in. Here’s the usual breakdown:

💡 The Multi Armed Bandit problem involves levers (‘arms’) that yield stochastic rewards that arise from unknown distributions. I have stuck with Gaussian distributions for this article, but there’s no reason why you couldn’t use other environments.

💡 The MAB problem depicts the tradeoff between exploration and exploitation of the levers. Different algorithms can be used to play the game in different ways.

💡 The epsilon-greedy algorithm provides a simple way to play the game. The player can alter the value of ε: the larger the value, the more exploration, albeit at the cost of less exploitation.

Training complete!

I hope you enjoyed reading as much as I enjoyed writing 😁

Do leave a comment if you’re unsure about anything, if you think I’ve made a mistake somewhere, or if you have a suggestion for what we should learn about next 😎

Until next Sunday,

Ameer

P.S… like what you read? If so, feel free to subscribe so that you’re notified about future newsletter releases:

Sources

• My GitHub repo where you can find the code for the entire newsletter series: https://github.com/AmeerAliSaleem/machine-learning-algorithms-unpacked

• “Reinforcement learning: An Introduction”, by Richard S. Sutton and Andrew G. Barto: https://web.stanford.edu/class/psych209/Readings/SuttonBartoIPRLBook2ndEd.pdf (^ btw this is a GOATed resource for the theory of reinforcement learning)

• “Bandit Algorithms”, by Tor Lattimore and Csaba Szepesvari: https://www.cambridge.org/core/books/bandit-algorithms/8E39FD004E6CE036680F90DD0C6F09FC

• A great blog on the topic of Multi Armed Bandits: https://www.geeksforgeeks.org/multi-armed-bandit-problem-in-reinforcement-learning/

1. Assming that T is divisible by 3. But you get the point.